
课程介绍

数学几乎是“艰难”与“枯燥”的同义词了,定理、推导,做题、考试,大脑的催眠药,意志力的催残剂。但数学又是如此重要,当绕过了它选择了工科,却发现每一项重要的应用背后都需要它的支撑。学习计算机,不管是基本的程序逻辑还是进阶的算法,都依托于某一项数学知识。
但是!数学又是一门无穷尽的学科,知识点与分支蜿蜒绵长。但CS的宝宝们,你们并不需要抱着数学书去啃!世界top大学有高招,比如!MIT 6.042J 就根据计算机方向所需的知识,对数学做了一个梳理打包,通过有趣的方式,让你快速构建CS所需最小数学知识根基!

MIT 6.042J 是顶级院校麻省理工出品的工科基础优质课程,围绕计算机科学方向,构建所需的数学体系内容,包含函数、离散数学、概率论、图和树结构,以及部分算法(例PageRank)。不同于枯燥的理论数学,本课程的数学知识都有计算机科学方向的延展应用,是工科方向同学值得一学的基础课程。

课程讲师 Albert R Meyer 是麻省理工 Department of Electrical Engineering and Computer Science (电气工程和计算机科学系)的教授。
课程主题
课程覆盖范围大致分为三部分。学完完成6.042J后,你能够解释和应用计算机科学中离散(非连续)数学的基本方法,并在算法设计和分析、可计算理论、软件工程、计算机系统等领域得到充分应用。
- 数学的基本概念:定义、证明、集合、函数、关系
- 离散结构:图,状态机,模运算,计数
- 离散概率理论
课程资料 | 下载

扫描上方图片二维码,关注公众号并回复关键字 🎯『6.042J』,就可以获取整理完整的资料合辑啦!当然也可以点击 🎯 这里 查看更多课程的资料获取方式!

ShowMeAI 对课程资料进行了梳理,整理成这份完备且清晰的资料包:
- 📚 课件:4个单元,111份,覆盖所有课程视频
- 📚 作业练习:12份作业,学后练手的好素材
- 📚 课内问题总结:35份文档,152个常见学习问题与解答
- 📚 拓展阅读材料:35份文档,覆盖所有chapter
课程视频 | B站
ShowMeAI 将视频上传至B站,并增加了中英双语字幕,以提供更加友好的学习体验。点击页面视频,可以进行预览。推荐前往 👆 B站 观看完整课程视频哦!
ShowMeAI选取2015年课程,是MIT全网开放的课程最新版本,公布的资料非常完备(电子书、课件、练习、考试和答案等),也最广为人知,有不少的学习打卡和网络笔记资源。
| Unit 1: Proofs | 对应书籍章节&测试题 |
|---|---|
| 1.1 Intro to Proofs | Chapter 1.1-3.5 | Problem Set 1 |
| 1.2 Proof Methods | |
| 1.3 Well Ordering Principle | |
| 1.4 Logic & Propositions | |
| 1.5 Quantifiers & Predicate Logic | Chapter 3.6-4.2 | Problem Set 2 |
| 1.6 Sets | |
| 1.7 Binary Relations | Chapter 4.3-5.3 | Problem Set 3 |
| 1.8 Induction | |
| 1.9 State Machines- Invariants | Chapter 5.4-7 | Problem Set 4 |
| 1.10 Recursive Definition | |
| 1.11 Infinite Sets |
| Unit 2: Structures | 对应书籍章节&测试题 |
|---|---|
| 2.1 GCDs | Chapter 8.1-8.10 | Problem Set 5 |
| 2.2 Congruences | |
| 2.3 Euler's Theorem | |
| 2.4 RSA Encryption | Chapter 8.11-9.4 | Problem Set 6 |
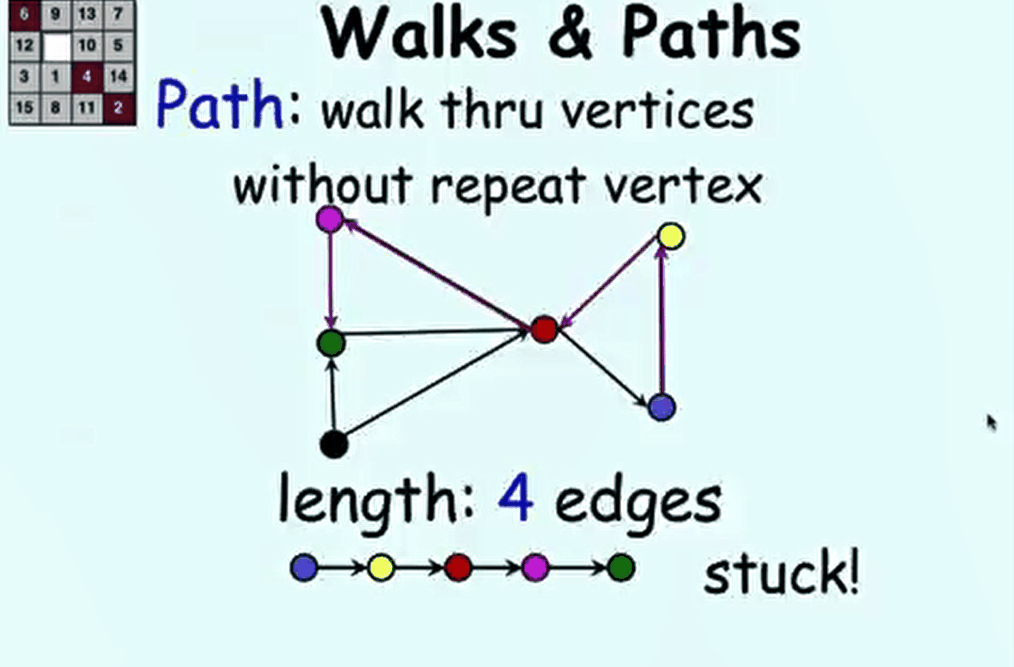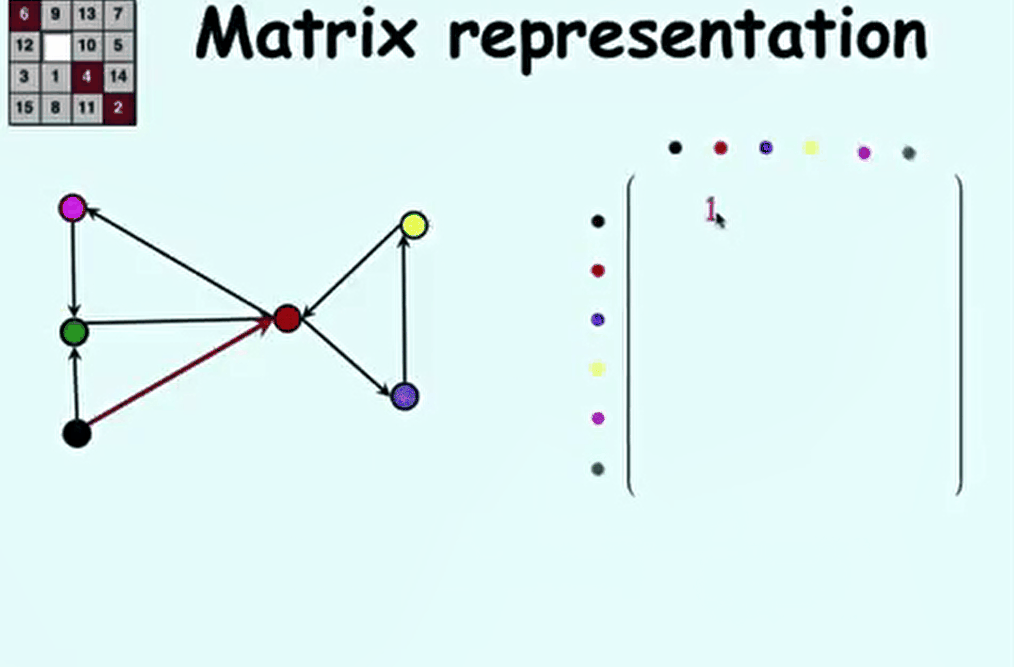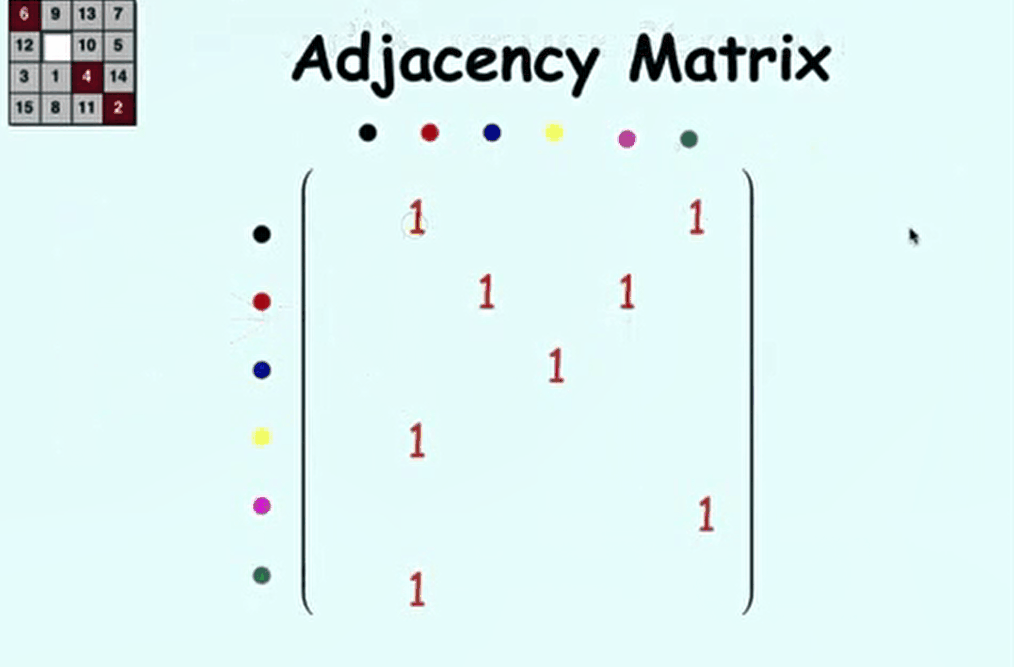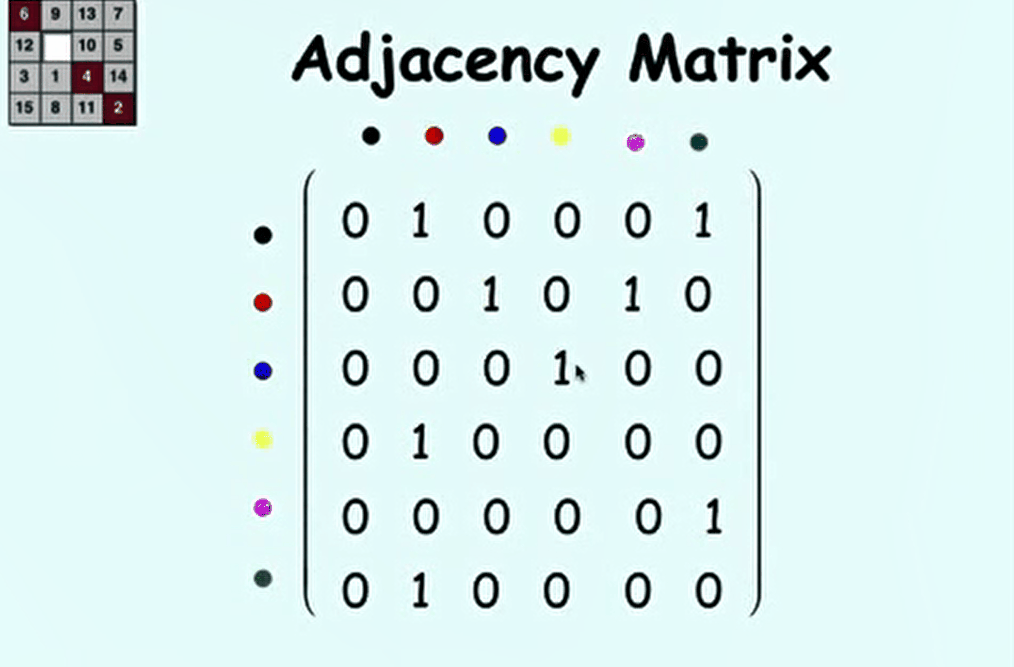
| 2.5 Digraphs: Walks & Paths | |
| 2.6 Directed Acyclic Graphs (DAGs) & Scheduling | Chapter 9.5-11.4 | Problem Set 7 |
| 2.7 Partial Orders and Equivalence | |
| 2.8 Degrees & Isomorphism | |
| 2.9 Coloring & Connectivity | Chapter 11.5-11.10 | Problem Set 8 |
| 2.10 Trees | |
| 2.11 Stable Matching |
| Unit 3: Counting | 对应书籍章节&测试题 |
|---|---|
| 3.1 Sums & Products | Chapter 13.1-13.7 | Problem Set 9 |
| 3.2 Asymptotics | |
| 3.3 Counting with Bijections | Chapter 14.1-14.8 | Problem Set 10 |
| 3.4 Repetitions & Binomial Theorem | |
| 3.5 Pigeonhole Principle, Inclusion-Exclusion |
| Unit 4: Probability | 对应书籍章节&测试题 |
|---|---|
| 4.1 Intro to Discrete Probability | Chapter 16.1-17.5 | Problem Set 11 |
| 4.2 Conditional Probability | |
| 4.3 Independence & Causality | Chapter 17.7-18.5 | Problem Set 12 |
| 4.4 Random Variables, Density Functions | |
| 4.5 Expectation | |
| 4.6 Deviation: Markov & Chebyshev Bounds | Chapter 19.1-20.2 |
| 4.7 Sampling & Confidence | |
| 4.8 Random Walks & Pagerank |
💡 说明1:课程视频详见B站。原视频数量为111个,上传时将4.5、4.6、4.7、4.8小节内的视频进行了顺序合并。
💡 说明2:B站的视频保留了MIT原始视频的小节序号(是的,偶尔有跳号现象[如1.2.1直接到1.2.3])。
💡 说明3:课件获取方式见文末。课件的命名follow对应视频的小节序号&命名,与官网信息保持一致(是的,有些课件的命名和内部topic不完全一致)。
更多技术与课程清单 | 点击查看详细课程
